＜付加行列法による逆行列計算と連立方程式のアルゴリズム＞

(例)
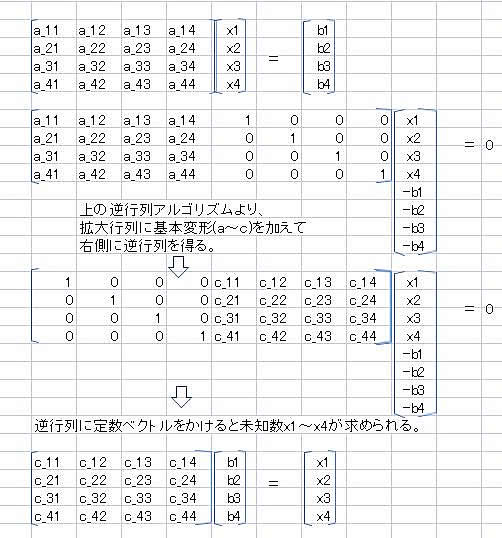
逆行列を求めたい正則行列を用意し、単位行列を付加した拡大行列を作り、下記のように各辺基本変形を行います。



＜連立方程式のアルゴリズム＞
連立1次方程式の解を求めることと逆行列を求めることと等価になる。
連立1次方程式を解く場合、単位行列を連結して拡大行列Mにしてみると よくわかります。



(（例） 逆行列を使った連立方程式の解


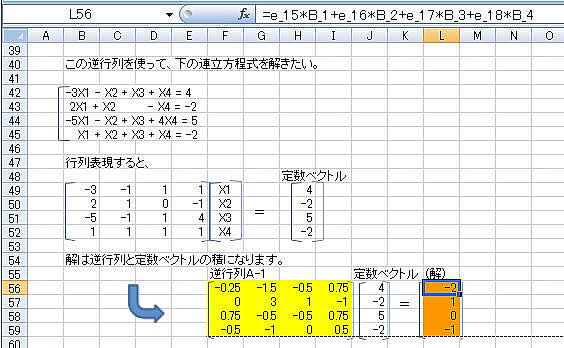
（計算方法の概略）
ｎｘｎ行列Ａ（正則）の右側にnxnの単位行列を連結nx2nの拡大行列A'を作る。
行列A'各行に対して行基本変形を適用して左側のnxn行列を単位行列に変形する。
列ｊを１にする。第１行から第ｎ行まで繰り返す。これを第１列から第ｎ列まで繰り返す。
全行基本変形が終わると、右側のnxn行列がAの逆行列A-1になる。

(1)Ａ'ij≠0の最初の行ｉ(i≧ｊ）を見つける。見つからない場合は、正則でない。
ｉ≠ｊならば第ｉ行と第ｊ行を入れ替える。（行列の基本変形a）
(2)各行に１／Ａ'ｊｊをかける。これによりAの(ｊ,j)成分が１になる。（行列の基本変形b）
(3)1≦k≦nかつ、k≠ｊである各行kに対して、行基本変形（c）を使って、
第ｊ行の−Ａ'ij倍を第k行に加える。このステップで、第ｊ列第ｊ行以外の上下各成分が0になる。
(4)ｊ＜nならば、ｊに１を加えてステップ（３）に戻って繰り返す。

（行列の基本変形定義）
'(a)２つの行を入れ替える。
'(b)ある行に０でないスカラーをかける。
'(c）ある行のスカラー倍を別の行に加える。

（この変形で利用する定理）
ｎｘｎ行列Ｍについて、行基本変形を行った結果をＭ'とする。
このとき、単位行列に対して同じ行基本変形を行った結果のｎｘｎ行列をＥとすると、
Ｍ'=ＥＭが成り立つ。

〈 戻る 〉