（座標変換の計算例）





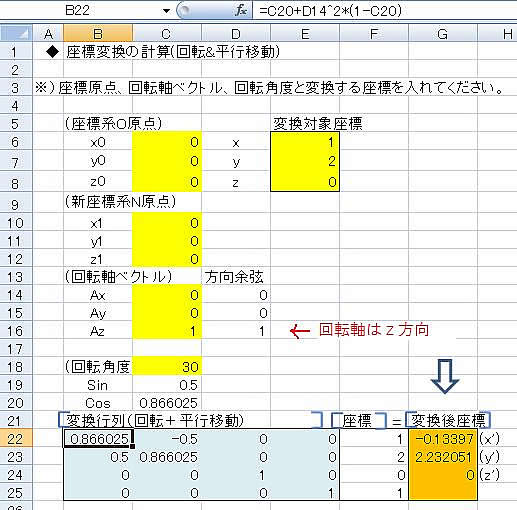
（ステップごとの計算内容は、数式確認できます。）

軸Aの方向は、この例ではz軸になっていますが、方向余弦を与えることで、任意方向の軸周りの
回転+平行移動が一発で計算できます。

＜３D座標変換のアルゴリズム＞

ベクトルP（座標(x,y,z)）を単位ベクトルAの軸周りに角度θだけ回転させ、その後、
ｄだけ平行移動させることを考える。
(回転変換)
一般にｘｙ平面上のベクトルPをz軸周りにθ回転させたP'は、元のPの成分を使って
次のように表わすことができる。
　 　　

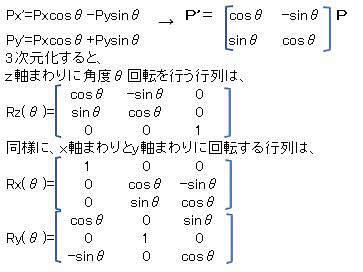
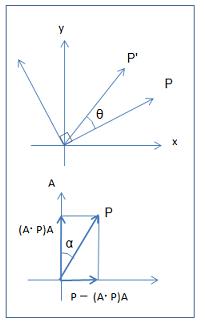
次に、ベクトルＰを任意の軸Ａの周りに回転させる場合を考える。
回転軸AとベクトルPのなす角度をαとする。
PをA上に射影したベクトルは、Aが単位ベクトルであるので、
Pja = （A・P）A
Aに関するPの垂直成分は、
Ppa = P - (A・P)A
このPpaを角度θだけＡｘＰ方向に回転する場合の回転式は、Pjaを加えて
Ｐ' ＝ Ｐcosθ＋ (A x P)sinθ + A(A・P)(1-cosθ)
と表わされるので、これを複合化して回転行列Mを作成する。

（4次元変換化）
これに平行移動のベクトルを追加すると回転移動の操作を一つの変換行列で表わすことができる。
べクトルを４次元に拡張して、第４の座標位置に平行移動Ｔに対応する成分を入れると、
回転移動を１つの変換行列として扱えるので便利である。


〈 戻る 〉