





■概要
3次元空間での座標変換(平行移動、回転、倍率変更、及び任意軸周りの回転移動による座標変換 )を行います。シート上の座標データだけでなく、メタセコイアなどモデリングソフトで出力された3Dモデル形状データも、物体の座標変換前後の形状を透視変換を用いて3D表示し、変換による変化を視覚的に確認できます。
■(1)平行移動、回転、倍率変更
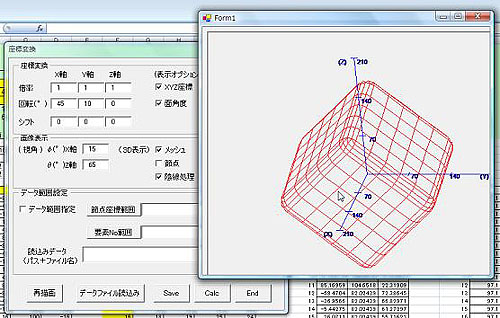
形状データ読込み後、座標変換のパラメータ(倍率、回転、シフト)数値を変えて、再表示を繰り返すことができます。
モデルの表示は、視角を変えたり、陰線処理を入れたりして、希望の角度での状態確認が可能です。このとき、計算結果シートには、座標変換前後のモデルの要素ごとの節点の座標、面角度が表示されるので、座標変換による各部の変化を数値的に評価するときに便利です。
出力画像は、再描画ボタンでExcelシート上に簡単にコピーできます。
(回転1)
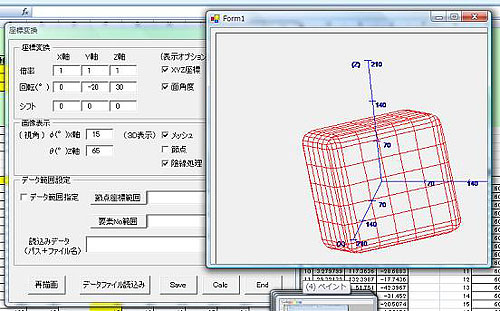
(回転2)
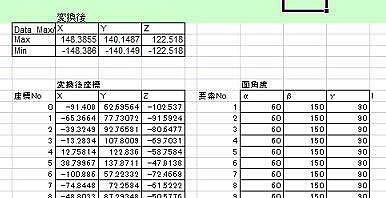
(座標変換後の座標 )
■(2)任意軸周りの回転移動による座標変換(追加)
(例) XYZ座標データAi (xi,yi,zi), i =1~n について、N(50,0,50)点を通る回転軸ベクトルC(1,1,1)の周りに60°回転したときの各点の座標Bi (Xi,Yi,Zi), i=1 ~nを計算します。)
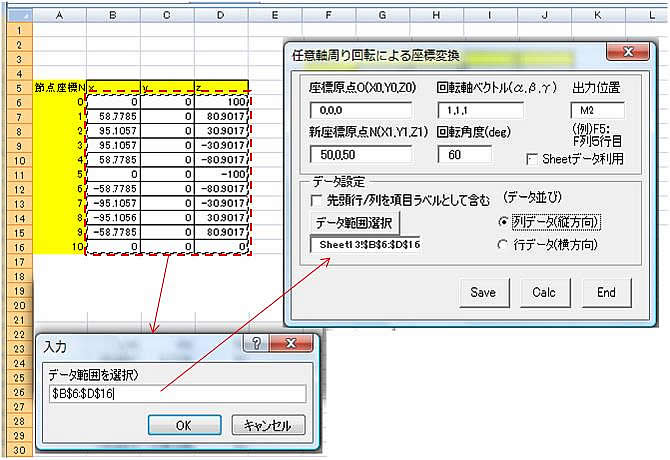
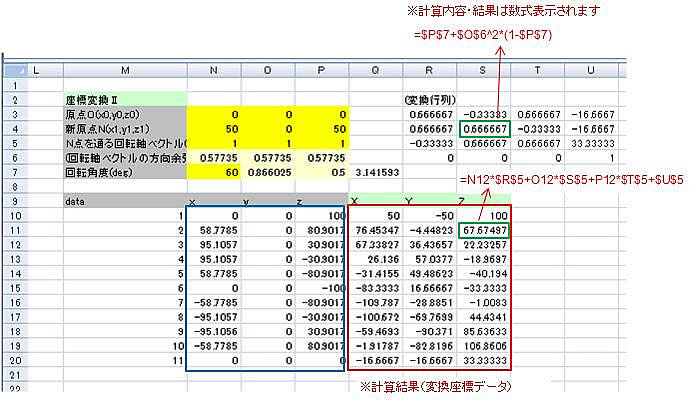
※座標変換結果は、シート上の指定位置に設定条件とともに数式入りで表示されます。
また、3D座標変換プログラム(1)を使って変換前後の形状を下記のように確認できます。
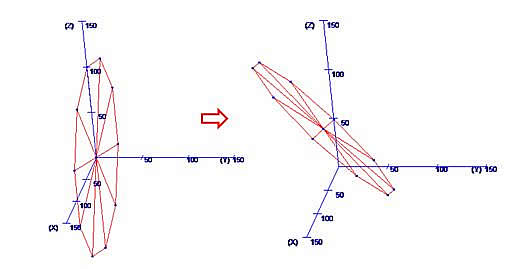
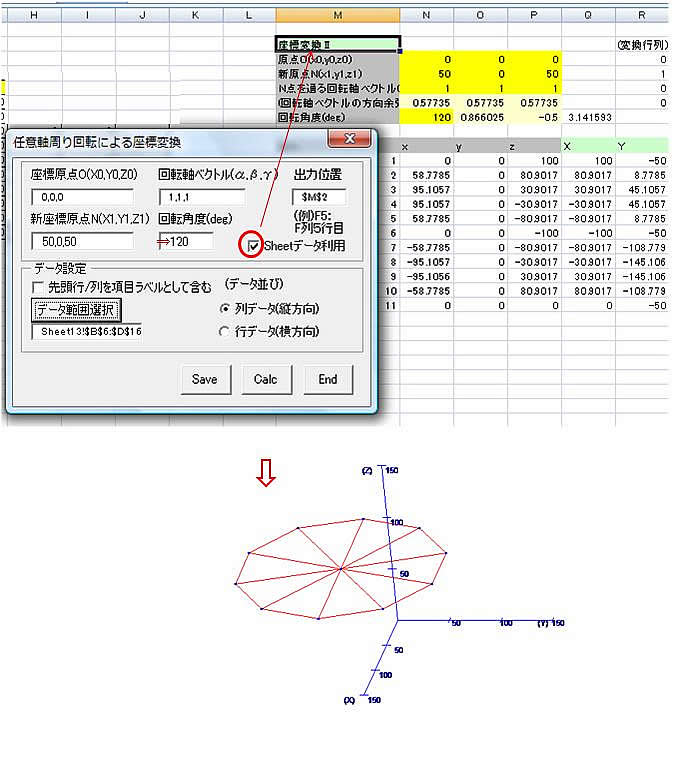
※条件変更の場合も、シート上設定データを使って簡単に出力できます。
(下の例では、回転角度を120°にして再計算させた場合)
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****