
■例4
<4>梁の強制振動/インパルス加振によるモード解析(両端単純支持) (※購入版のみ対応)
Fourier級数展開の手法を使って、両端単純支持された長さLの梁の1点にインパルス加振した場合の振動モードを解析します。(理論式の詳細は、説明書参考文献を参照ください)
梁に強制振動f(x,t)が働いている場合、偏微分方程式は、次で与えられます。
![]()
ここで、ρ:密度、S:断面積、EI:曲げ剛性を表わします。
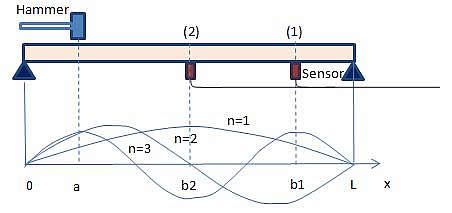
今、下図のように、単純支持梁の1点をハンマ-で打撃したときを考えます。
外力f(x,t)は、δ関数で次のように表わします。
![]()
この場合の偏微分方程式の解は、以下のようになります。
![]()
![]()
■手順
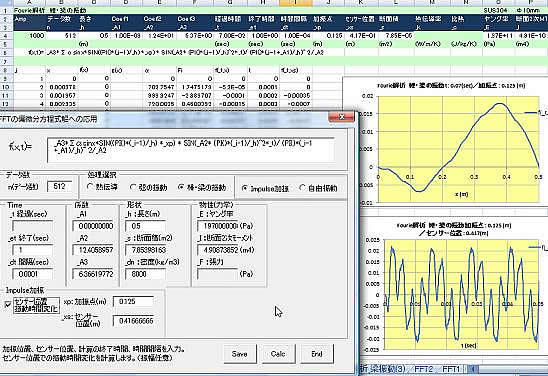
計算フォームから、”フーリエ変換/偏微分方程式解への応用/梁の振動/Impulse加振”を選択します。
関数f(x、t)に方程式の解、計算条件、物性値、境界条件、初期条件を下のように入力。→Calc
計算フォームの式、
_A3*Σαsinx*SIN((PI()*(_i-1)/_h) *_xp) * SIN(_A2* (PI()*(_i-1)/_h)^2*_t)/ (PI()*(_i-1+_A1)/_h)^ 2/_A2
は、フーリエ変換してα=Anが求められ、Excelシート上へ数式として展開、逆フーリエ変換して、その時刻の梁の変位分布が求められます。
計算は、棒のa点をハンマーで打撃し、(ⅰ)ある時刻における梁の変位分布(ⅱ)梁の上に置いたセンサー位置での変位の時間変化を求めています。また、ここでは(ⅱ)のセンサー位置(1)(2)による波形の違いを見ています。
■計算結果
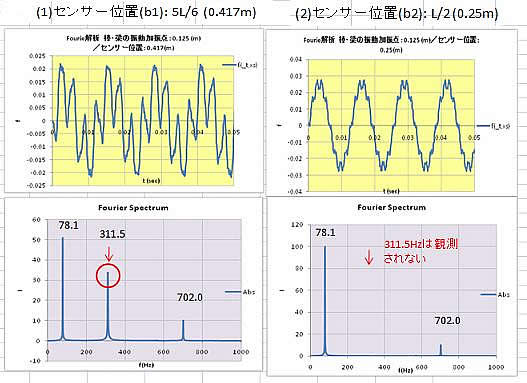
波形をスペクトル解析してみると、(ⅰ)では、固有振動モード1,2,3とも計算で求めた周波数と一致します。 一方、固有振動モード2の節にあたる位置にセンサーを設置した(ⅱ)の場合、そのモード2の振動数が消えていることが確認できます。このことは、固有振動モードの節位置では、その振動モードは観測できないことを示しています。
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****