





■概要
熱伝導、電界などLaplace方程式やPoisson方程式で表現されるポテンシャル問題の解析は、自然現象や工学上の問題では頻繁に使われます。このプログラムでは、境界要素法を用いた数値解析により、2次元Laplace方程式についての近似解を求めます。
境界要素法では、重み付き残差法を用いて微分方程式を満足する近似解を求めます。ここでは、重み関数に基本解であるグリーン関数を使い、領域内部についての微分方程式を境界を含む積分方程式へ変換します。この積分方程式を離散化して、連立1次方程式を解いて、未知な境界値、領域内部の任意の点の近似値を求めることができます。
モデル、境界条件の設定や変更が簡単にでき、また有限要素法のように領域全体を離散化する必要がなく、計算時間短縮やPCメモリ節約などメリットがあります。
■計算例(1) 平行平板電極表面の段差による電位分布と電子軌道への影響調査
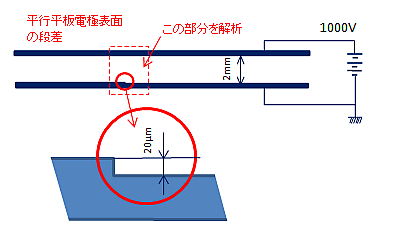
下図のように、真空中に置かれた平行平板電極のプラス側電極に高電圧を印加し、グラウンド電極表面から電子を発射する場合で、電子発射箇所の近くの電極表面に20μm程度の段差がある場合の電位分布と電子軌道への影響を調べます。
【データ入力】
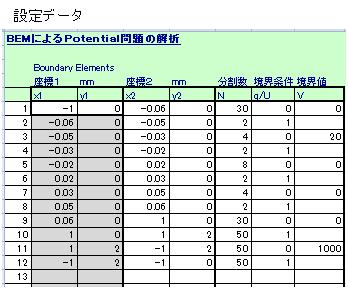
電極表面の段差がある部分付近(上図点線)を解析領域にとり、境界要素分割とデータ設定を行います。
境界要素の設定データは、下表のように任意の区間を指定しての分割数、境界条件、データを解析シートに記入して計算フォームから計算スタートさせます。
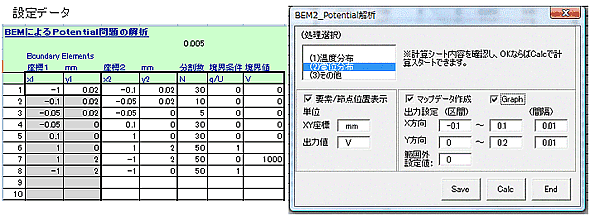
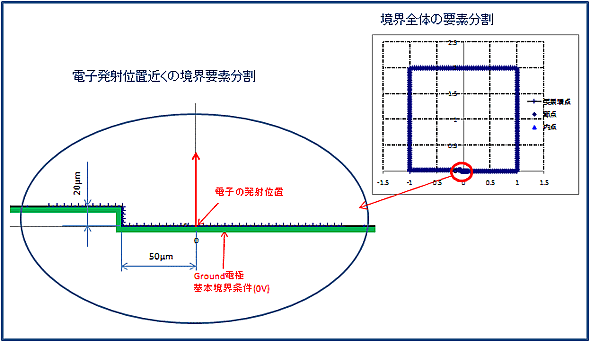
実際に分割された境界要素、節点の位置や分割のようすは下図のように出力され、モデルのデータ設定が正しくできていることをチェックできます。
【計算結果】
電位分布(段差付近)と電子軌道 (加速1000V、初速度0、段差から50μm位置)
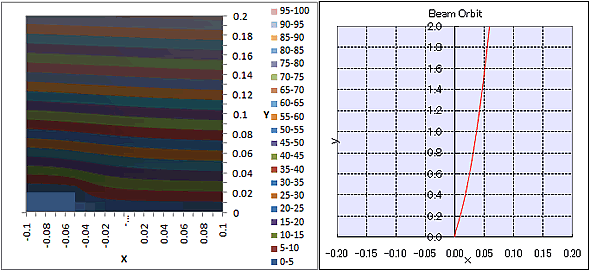
電極表面段差付近の電位分布の歪みが0.2mm程度上方でも影響しているのが分かります。
電極間電位差1000V、段差から50μm位置から初速度0で発射された電子の対向電極への到達位置(変位)は、x方向59μmになります。
(注:電子軌道は別計算により求めており、SUITEXLには含まれません)
■計算例(1)-2 平行平板電極に制御電極を付加したときの電位分布と電子軌道への影響調査
下図のように、真空中に置かれた平行平板電極のプラス側電極に高電圧を印加し、グラウンド電極表面から電子を発射する場合で、電子発射箇所の近くに設置した制御電極の電圧を変化させた場合の電位分布と電子軌道への影響を調べます。
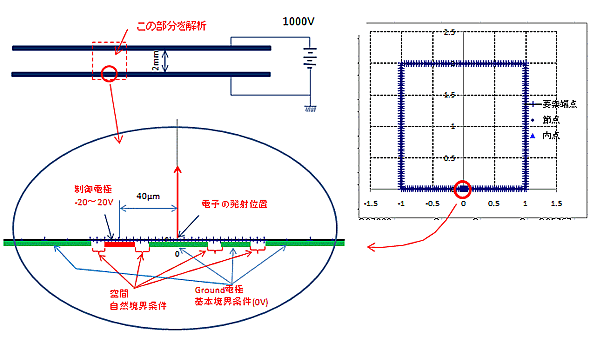
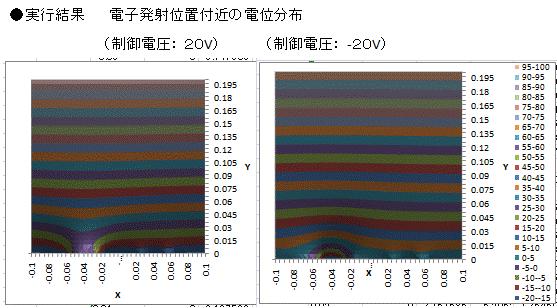
制御電極付近の電位分布の歪みは、制御電圧の正負大小で大きく変化していることが確認できます。電子発射位置にも影響しており、電圧が大きくなるとその程度も大きくなる傾向にあります。
電子軌道 (加速1000V、初速度0、制御電極中心から40μm位置)
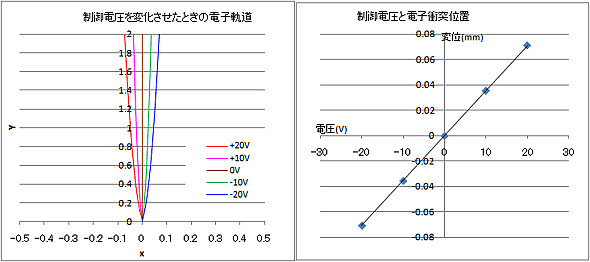
電子軌道解析により、発射された電子の対向電極への到達位置(変位)は、制御電圧に比例しており、20Vではx方向+71μmに達します。
(注:電子軌道は別計算により求めており、SUITEXLには含まれません)
■計算例(2) ■一様流中の円柱周りの流れ
下図のような一様流体中(2次元非圧縮流体、渦なし)の円柱周りの流れを計算します。
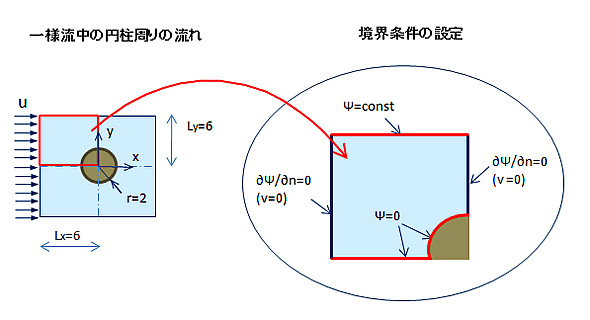
1)流体の流速 V=(u,v) は、流れ関数Ψを使って次のように表わされます。
u = ∂Ψ/∂y , v = ∂Ψ/∂x
また、渦度は、
ω=rot V = ∂v/∂x - ∂u/∂y = - (∂2/∂x2 + ∂2/∂y2 )Ψ = -∇2Ψ
すなわち、渦度ベクトルωはz軸と平行で、渦無し(ω=0)ではLaplace方程式∇2Ψ =0 が成立します。
2)境界条件を次のように設定します:
・y=0軸上と円柱表面で流れ関数 Ψ = 0、y= -6でΨ=一定値
・x=0, x= - 6 で∂Ψ/∂n=0 (境界に沿う流速 = 0)
3)BEMによる計算結果により流れ関数Ψの分布が得られ、また、その勾配((4)-3-①)から場所ごとの流速を計算できます。(理論式の詳細は、説明書、参考文献をご参照ください)
【データ入力】
解析シートに境界の要素分割データを入力します。
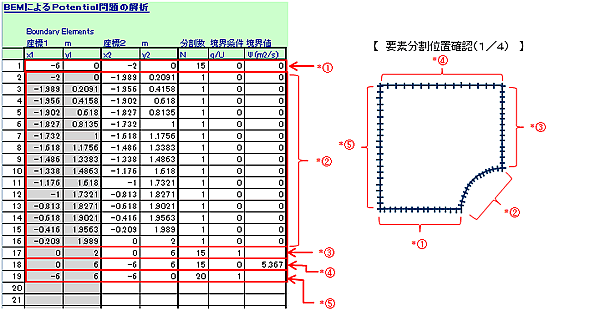
【計算結果】
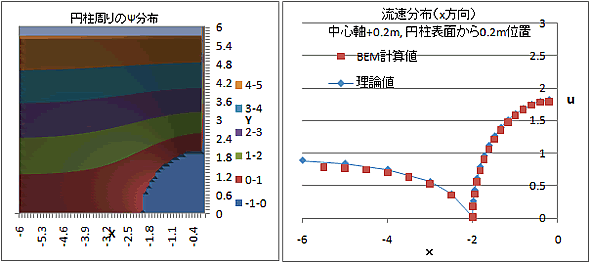
円柱周りのΨ分布が計算され、その分布傾きから中心軸付近から円柱周りの流速(x方向)を求め、理論値と比較したものを下図に示します。円柱付近の流速についても理論値に近い計算値が得られています。
■計算例(3) ■板材の温度分布(2次元)
下図のように横幅が不均一な長さLの板材の両端が高・低両熱源(温度がそれぞれT1,T2)に接続されているときの板材の定常状態における温度分布を求めます。(紙面に垂直方向の温度分布が無視できる場合)
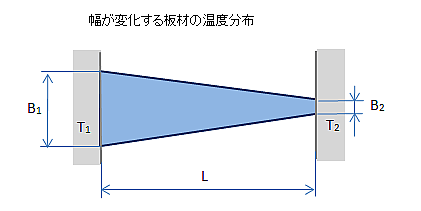
【データ入力】
解析シートに境界の要素分割と節点の設定、境界条件、内部解析ポイント位置などデータを入力します。
次の例では、T1=20℃、T2=150℃に固定して、定常状態に達したときの板材の温度分布を計算させています。分割要素位置や分割の細かさ、その変更など、下の解析シートのように簡単に設定できます。 特に解析したい箇所は、その付近の解析ポイントを増やすことで詳細に分析できます。
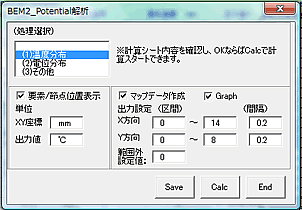
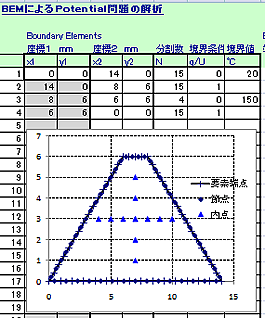
【計算結果】
定常状態における板材の温度分布をマップ化して表示します。部分的に詳細を計算したい場合は、マップ表示部分の指定と分割を細かくして同じ解析シートで何度でも繰り返し計算し、結果を即座に表示できます。
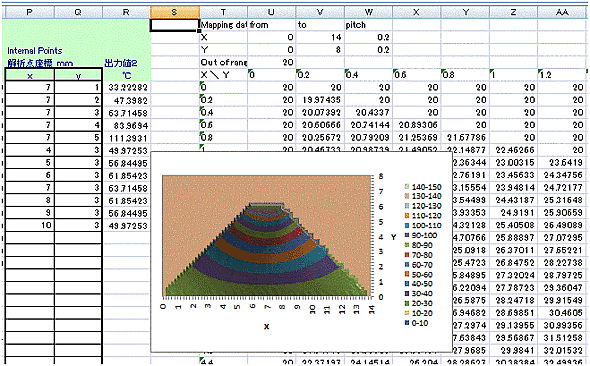
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****