
■概要 (※購入版のみ)
材料の振動解析や電気回路の過渡現象の解析、物性値の挙動など様々な場面で微分方程式を解いて特性を導き出したいことがあります。ラプラス変換法は、フーリエ変換の変数変換機能をうまく利用したもので、変換を適用することで微分方程式を簡単な代数計算に置き換えることができます。
このプログラムでは、目的モデルの微分方程式をラプラス変換した後の変換式を入力として、フーリエ逆変換ルーチンを使用して解を求めます。
計算結果として、複素数の計算過程が数式、グラフとともにExcelシートに表示されます。関数に留数(特異点)を持つ場合以外は、モデルに合せて自由にカスタマイズして計算することができます。
(計算例1)ランプ入力に対するL-R-C回路の応答
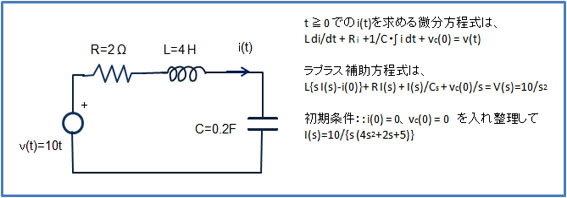 }
}
■手順
計算フォームから、”フーリエ変換/ラプラス変換への応用”を選択します。
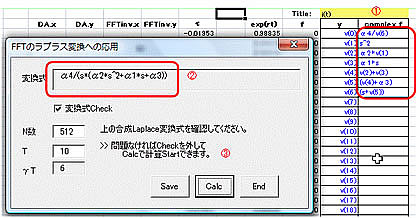
①解析フォームにラプラス変換された微分方程式の分解式を入力
②計算フォームで組み立て確認します。
③Calcで、フーリエ逆変換ルーチンを用いてラプラス逆変換の計算を行います。
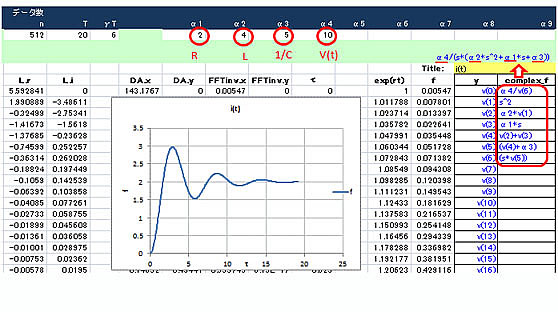
■計算結果
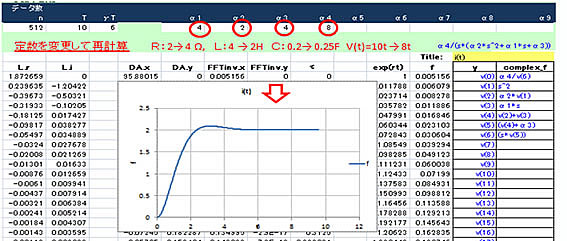
下図は、定数を変更して再計算させた例です。
(計算例2)強制振動系モデルの計算(共振を含む)
図に示すように、質量 m のおもりがバネ定数 k のバネの下端に取り付けられ、バネ上端は固定されているモデルについて、おもりがつり合い位置で静止している状態からt=0で強制振動が加えられる場合のおもりの運動を計算させます。
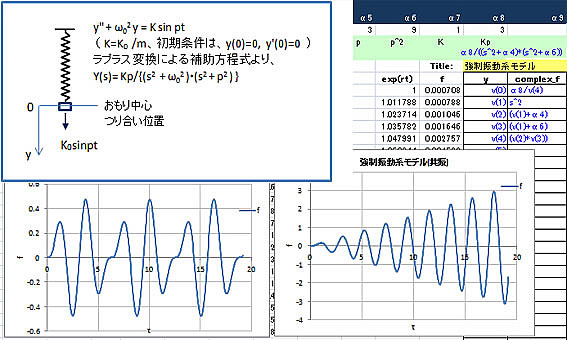
結果は、2つの調和振動の重ね合わせになります。(右図は、共振時の結果を示します)
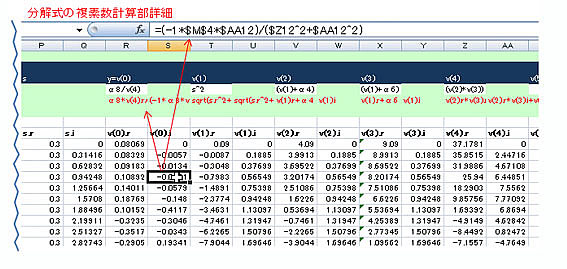
(計算例3)衝撃荷重(急速荷重)応答の計算
次の図に示すように、両端が単純支持された梁の中央に突然外力Pが(1)矩形パルス(2)半sin波型として作用する場合の梁の応答を計算します。
(ここで、梁は1000X100X10mm/SUS304材、外力は100N、50msec、衝撃による変形は、弾性変形範囲内とします。)
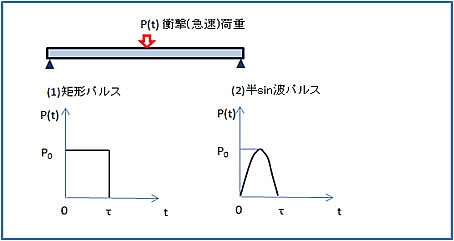

(計算結果)
(1)矩形パルス衝撃の場合
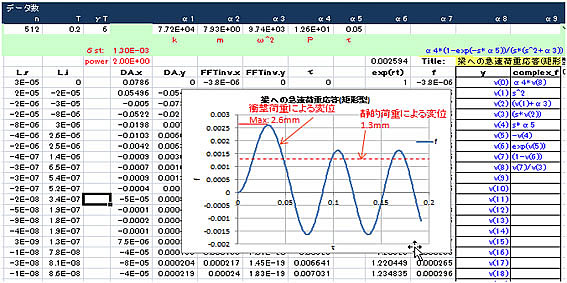
(2)半Sin波型衝撃の場合
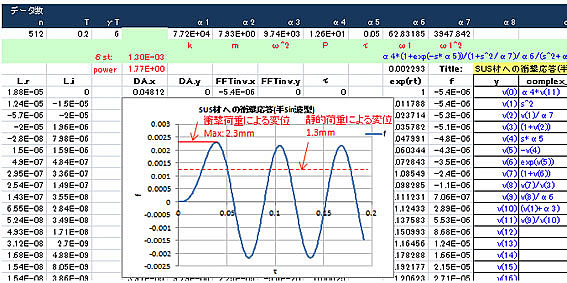
この場合の衝撃による動的変形量の最大値は、静的荷重の場合の2倍程度になり、パルス形状により動的振幅が異なることがわかります。
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****