
■概要 (※購入版のみでご利用いただけます)
一般に偏微分方程式を解析的に解く場合、式に変数分離法を適用し、変数ごとに常微分方程式に落とし込んで、モデルの境界条件と初期条件を満たすように解を導きます。
このプログラムでは、熱伝導、振動など、偏微分方程式が支配する物理・工学現象のモデルについて、計算フォーム上でそれぞれの理論式、数式を変更、カスタマイズして解析することができます。
(但し、方程式が変数分離できて、解がsin級数で展開できるような境界条件を適用できる場合。理論式の詳細は、説明書・参考文献を参照ください)
<1>熱伝導解析(1次元非定常、両端固定温度の側面断熱とみなすことができる場合)
■例
長さLの棒を温度T(x)に加熱した後、時刻0でその両端を温度T0、TLで固定した場合、棒の温度分布の時間推移を求めたい。
1次元熱伝導方程式
![]()
を、境界条件:u(0,t)=T0、(L,t)=TL、と初期条件:t=0でu(x,t)=f(x)の元に変数分離法を使って解きます。
解は、 ![]() 、
、
このとき、係数Bnは、u(x,0)がf(x)のフーリエSin級数の係数になるように決定されます。
![]()
■手順
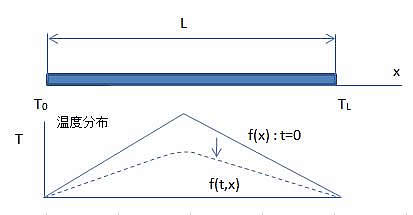
計算フォームから、”フーリエ変換/偏微分方程式解への応用/熱伝導”を選択します。
関数f(x、t)に方程式の解、計算条件、物性値、境界条件、初期条件を下のように入力。→Calc
計算フォームの式、Σαsinx*exp(-1*_k/_c/_dn*(PI()*(_i-1)/_h)^2*_t)は、フーリエ変換してα=Bnが求められ、Excelシート上へ数式として展開、逆フーリエ変換して、その時刻の温度分布が求められます。
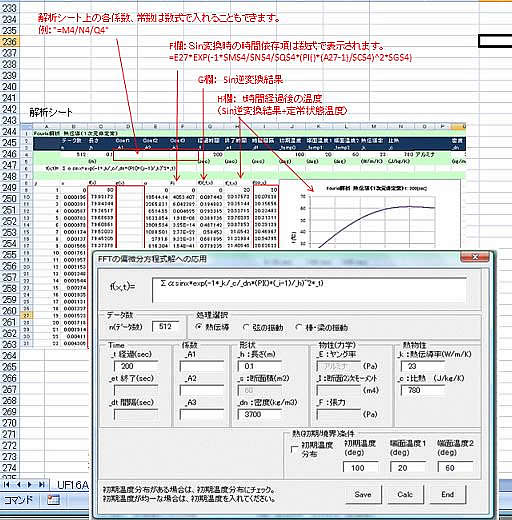
■計算結果
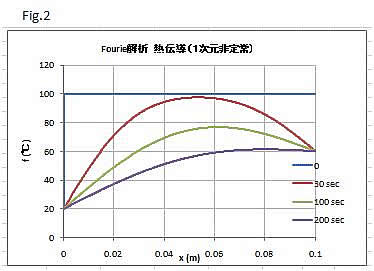
解析シートとともに、計算結果のグラフが出力されます。経過時間_t(sec)を変えてそれぞれデータを得るので、まとめると、棒の長さ方向の温度分布の経過時間による推移グラフが得られます。
この例では、初期温度分布を一様としましたが、直接解析シートに温度分布を入力して、そこから計算スタートできます。物性値や長さ、経過時間を変えて目的時刻での温度分布が得られます。
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****