

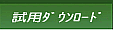




■概要
2つの変数が正規分布をしていないデータについて相関係数を求めたい場合、データを順位だけのデータに変換して相関係数を求める方法があり、スピアマン(Spearman)の順位相関係数やケンドール(Kendall)の順位相関係数がよく使われています。 このプログラムでは、1組のデータについて順位相関係数と有意確率(p値)を算出します。
【例】下表は、9カ国の平均年間労働時間と一人当たりの国民所得について調べたものである。両者の相関について、(1)Spearmanの順位相関係数と(2)Kendallの順位相関係数を求め、またその有意確率を求める。
■スピアマン(Spearman)の順位相関
(ⅰ)リスト各データの大きさから、それぞれ順位を付ける(同順位がある場合はTie補正する)
(ⅱ)各データ組の順位差の2乗和から相関係数rsの計算
(ⅲ)有意確率(両側)を計算
(Ⅳ)Peasonの相関係数を計算(参考)
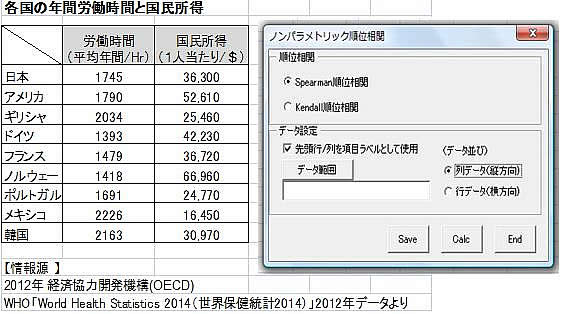
このSpearmanの順位相関係数rsは、順位データについてのPeasonの線形相関係数であり、その rsが0でないことの有意性は下記 t 値で検定できます。 これは近似的に自由度ν=N-2 のStudent分布 A(t/ν) に従うので、このプログラムでは下記 z=ν/(ν+ t2) についての不完全ベータ関数 Iz(ν/2,1/2)=1- A(t/ν) から有意確率を計算しています。
注)Student分布A(t/ν) は、二つの分布が同じ平均値を持つかどうかの検定に用いられ、1- A(t/ν) が『平均値は等しい』という仮説を棄却する有意水準になっている。
⇒結果:順位相関係数:-0.65、有意確率0.058で負の相関が認められます。
■ケンドール(Kendall)の順位相関
(ⅰ)リスト各データの大きさから、それぞれ順位を付ける(同順位がある場合はTie補正する)
(ⅱ)相関係数の計算
N(N-1)/2通りのデータ対それぞれに2つのxの大小関係と2つのyの大小関係が同じ向き(同順の数P)と逆 向き(逆順の数Q)に分けて、相関係数τ=2(P-Q)/{N(N-1)}を計算する。
(ⅲ)有意確率(両側)を計算
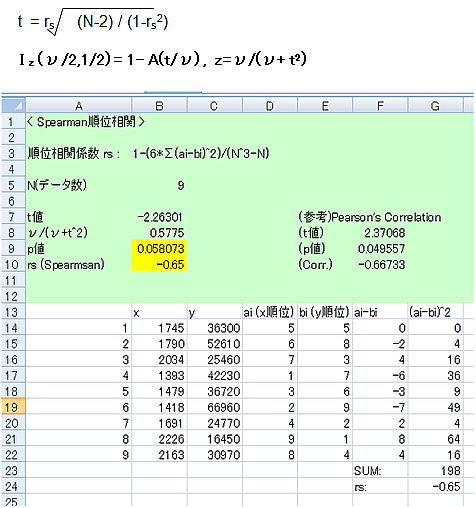
計算された相関係数τは、平均0、分散=(4N+10)/{9N(N-1)}の正規分布に近似的に従うことから、相関係数τが標準偏差の何倍に隔たっているかをz値とするとき、その相補誤差関数から両側有意確率を計算する。
(Ⅳ)Peasonの相関係数を計算(参考)
⇒結果:順位相関係数:-0.50、有意確率0.061で負の相関が認められます。
![]()
■概要/メニュー/使い方
■プログラム
・関数フィッティング
多項式近似曲線
多項式近似曲面
非線形関数
3次Spline補間曲線 (New)
双3次補間曲面 (New)
コンター図作成 (New)
・積分/表面積・体積
関数の積分
回転体の側面積・体積
・線分長さ
重積分(モンテカルロ法)
表面積計算(3D要素分割)
複雑形状の面積
・方程式の解
連立1次方程式
非線形方程式(1変数)
1階常微分方程式
連立微分方程式
・高階微分方程式
・ベクトル解析
行列計算1
(行列式/逆行列/積)
行列計算2
(固有値/固有ベクトル)
3D座標変換
3D関数
・フーリエ解析
スペクトル解析
偏微分方程式解へ応用
①(熱伝導解析)
②(弦の振動解析)
③(梁の振動解析)
④梁のImpulse加振モード解析)
⑤ラプラス変換へ応用
・統計解析
ヒストグラム作成(複数)
正規性の検定
相関分析(無相関検定)
区間推定
(母平均/比率)
仮説の検定
(母平均/母比率/適合度)
差の検定
(母平均/母比率/等分散性)
ノンパラメトリック検定
(Wilcoxon検定)
ノンパラメトリック順位相関
(Spearman / Kendall )
順列・組合せ
重回帰分析
・タグチメソッド
静特性
(望目/ゼロ望目/望小/望大)
動特性
・Fileデータ処理
データ検索・抽出・編成
Outlook mailデータ取出し
・シミュレーション
BEM_梁曲げ解析
Potential問題解析
*****